Word2Vec (Skip-gram) 모델의 개선 방법
개요
현재 진행중인 NLP 스터디에서는 매주 돌아가며 논문을 한 편씩 공부하고 있다. 이번주에는 Distributed Representations of Words and Phrases and Their Compositionality 논문을 공부하였으며, 이 글에서는 스터디를 준비하며 공부한 내용을 올려보고자 한다. 참고로 아래 논문은 내용이 너무나(필요 이상으로) 간결하게 설명되어 있어 읽기가 정말… 어려웠다.
이 논문에서는 단어 벡터화의 새로운 지평을 연 Word2Vec 모델, 그 중에서도 Skip-gram 모델의 계산량 개선에 대해 논의한다. Word2Vec은 T. Mikolov 및 그 외 연구진에 의해 쓰인 Efficient Estimation of Word Representations in vector space (2013) 논문에서 처음 도입되었으며, 해당 모델은 이 포스트에서 다룬 바 있다.
Skip-gram은 단어의 벡터 표현을 통해 다음과 같이 단어들 사이의 의미적, 형태적 관계를 담아낼 수 있다는 장점이 있다.
\[v_{\text{king}} - v_{\text{man}} + v_{\text{queen}} \quad \simeq \quad v_{\text{woman}}\]여기서 기호 \(\simeq\) 은 단어들에 대응되는 벡터 공간에서 좌변의 벡터와 가장 가까운(cosine similarity가 가장 높은) 벡터가 우변의 벡터라는 의미이다. 그러나 손실 함수의 그래디언트를 계산할 때마다 모든 단어에 대한 \(\exp\) 함수값을 구해야하므로 계산량이 과도하다는 단점이 있다.
이 논문에서는 Skip-gram 모델의 계산량을 줄이기 위한 방법으로 계층적 소프트맥스, 네거티브 샘플링, 빈도에 따른 서브샘플링을 소개하고 있으며, 또한 New York Times, Korean Air 등 두 단어 이상의 길이를 가지는 구절을 토큰화하는 방법에 대해서도 논의한다.
Hierarchical Softmax
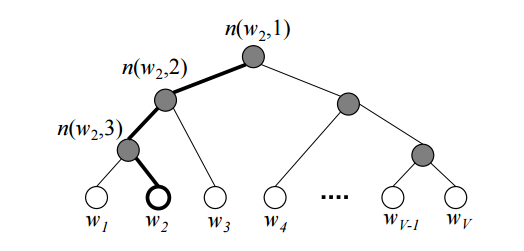
계층적 소프트맥스(hierarchical softmax)는 기존 소프트맥스를 대신하여 가능한 출력별 확률을 계산하는 모델이다. 이 모델은 이진 트리를 사용하여 모든 단어를 표현한 후 해당 단어에 도달할 확률을 구해나간다. 트리의 각 잎(leaf, 트리의 말단)은 단어에 해당하며, 뿌리(root)로부터 각 잎까지는 유일한 경로(path)로 연결된다. 이 모델은 단어의 입력 벡터만 존재하며, 대신 트리의 각 마디(node)에 대응되는 벡터가 존재하여 이를 훈련시키도록 한다. 각 마디에서는 왼쪽과 오른쪽 중 어떤 자식을 선택할 지에 대한 확률이 주어진다.
[image source](https://shuuki4.files.wordpress.com/2016/01/hsexample.png)
주어진 훈련 텍스트에 등장하는 단어들의 집합을 Vocab이라 하고, 이 집합의 크기를 \(K\) 라고 가정한다. \(L(w)\)를 뿌리로부터 단어 \(w\)까지 도달하는 경로의 길이라고 하고, \(n(w,i)\)를 뿌리부터 단어 \(w\) 사이의 경로(유일함!) 중 \(i\)번째 마디라고 정의하자. 따라서 \(n(w,1)\)은 뿌리에 해당하고, \(n(w,L(w))\)는 단어 \(w\) 자신이다. 내부 마디 \(n\)마다 자식 하나를 임의로 고정하고 이를 \(ch(n)\)이라 표기하자.
이제 중심 단어 \(w_i\)의 문맥에 단어 \(w\)가 등장할 확률은 다음과 같이 정의한다:
\[p(w|w_i) =\prod_{j=1}^{L(w)-1} \sigma([n(w,j+1) = ch(n(w,j))]\cdot {u_{n(w,j)}}^t v_{w_i}).\]여기서 \([x]\)는 \(x\)가 참일 때 \(1\), 거짓일 때 \(-1\)로 주어지는 함수이며 \(\sigma\)는 시그모이드 함수이다. 그리고 \(v_{w_i}\)는 단어 \(w_i\)의 입력 벡터, \(u_{n(w,j)}\)는 내부 마디 \(n(w,j)\) 의 벡터 표현이다.
이렇게 정의된 확률은 어떤 의미를 가지는 지 생각해보자. 뿌리부터 단어 \(w\) 사이 임의의 내부 마디 \(n\)에 대해, 해당 마디의 고정된 자식 \(ch(n)\)은 왼쪽이라고 가정하자. 그리고 왼쪽 자식으로 진행할 확률 \(p(n, \text{left})\)을 다음과 같이 정의하자.
\[p(n, \text{left}) = \sigma({u_n}^t v_{w_i})\]그러면 해당 값은 위에서 정의된 함수의 component인
\[(\star) \qquad \sigma([n(w,j+1) = ch(n(w,j))]\cdot {u_{n(w,j)}}^t v_{w_i})\]와 일치함을 알 수 있다. 마찬가지로 \(n\)에서 오른쪽 자식으로 진행할 확률 \(p(n, \text{right})\)을 생각하면
\[p(n, \text{right}) = 1 -p(n, \text{left}) = 1- \sigma({u_n}^t v_{w_i})\]이다. 시그모이드 함수는 임의의 \(x\)에 대해 \(1 - \sigma(x) = \sigma(-x)\) 를 만족하므로,
\[p(n, \text{right}) =\sigma(-{u_{n}}^t v_{w_i})\]이고, 역시 위의 등식 (\(\star\))이 성립한다.
따라서 앞서 정의된 확률 \(p(w\vert w_i)\)는 뿌리로부터 단어 \(w\)에 도달할 확률임을 알 수 있다. 임의의 단어는 뿌리에서부터 연결되어 있으며, 또한 뿌리에서 출발하면 결국 어떤 단어에 도달하게 되므로 자연스레 다음 식을 얻을 수 있다.
\[\sum_{w=1}^{K} p(w|w_i) = 1\]따라서 \(p(w\vert w_i)\) 는 확률분포를 이루게 된다! 기존 Skip-gram 모델에서 계산량이 증가함에도 불구하고 소프트맥스 함수를 적용하는 이유 또한 각 단어의 예측 확률의 합이 \(1\) 이 되어 확률 분포를 이루고, 이로 인해 추정이 가능해지기 때문이다. 따라서 우리는 기존 Skip-gram 모델에서 소프트맥스 함수를 이용하여 \(\hat{y}\)를 계산하는 과정을 위에서 정의한 계층적 소프트맥스를 이용하여 대체할 수 있다.
계층적 소프트맥스 모델의 손실 함수는 \(-\log(p(w\vert w_i))\) 로 주어지며, 해당 함수의 그래디언트는 \(L(w)\) 정도의 항을 계산하여 구할 수 있다. 다만 여기서는 출력 벡터를 업데이트하는 것이 아니라 트리의 내부 마디들의 벡터를 업데이트하게 된다(참고로 내부 마디의 갯수는 \(K-1\)개). 이렇게 정의된 모델은 계산량이
\[\text{Average}_{w}(L(w)) \sim \log_2 (K)\]에 비례하므로 기존 소프트맥스 모델에 비해 획기적으로 줄어들게 된다.

[image source](http://homes.sice.indiana.edu/yye/lab/teaching/spring2014-C343/images/Huffman-tree-Fig5.24.png)
본 논문에서는 Huffman 트리를 이용하여 계층적 소프트맥스를 구현하였다. Huffman 트리는 가장 빈도가 낮은 단어부터 두개씩 묶어가면서 전체 단어를 연결하여 생성한다. 따라서 가장 빈도가 높은 단어가 가장 마지막에 묶이게 되므로 트리의 뿌리로부터 가깝게 생성된다.
Negative Sampling
네거티브 샘플링은 계층적 소프트맥스의 대안으로 사용할 수 있는 방법이다. 매 훈련 스텝마다 모든 단어에 대해 연산을 수행하는 소프트맥스와는 달리, 정해진 갯수의 부정적 예제만을 샘플링하여 이 단어들의 등장 확률을 감소시키는 방향으로 훈련하는 방법이다.

[image source](https://slideplayer.com/slide/11911312/67/images/19/Skip-Grams+with+Negative+Sampling+%28SGNS%29.jpg)
주어진 중심 단어 \(c\)와 임의의 단어 \(w\)에 대해, \(w\)가 \(c\)의 문맥에 등장할 확률을 \(p(w\vert c)\)라 하자. \(c\)의 문맥에 등장하는 단어 \(o\), 그리고 \(c\)의 문맥에 등장하지 않는 단어들(negative samples) \(k\)개로 이루어진 집합 \(\{w_1,\ldots, w_k\}\)를 생각하자. 이때의 목표는 \(p(o\vert c)\)는 증가하고 \(p(w_i\vert c)\)는 감소하는 방향으로 모델을 훈련하는 것이다. 다시 말하면 \(p(o\vert c)\) 와 \(1-p(w_i\vert c)\) 가 모두 증가하길 바라는 것이다. 이를 정리하면 다음과 같다.
\[\begin{array}{lcl} (\star \star) &&\text{maximize} \log\left(p(o\vert c) \cdot \prod_{i=1}^{k}(1-p(w_i\vert c)) \right) \\ &= &\text{maximize} \left(\log p(o\vert c) + \sum_{i=1}^{k}\log(1-p(w_i\vert c) \right) \end{array}\]기존 Skip-gram 모델과 동일하게 단어 \(w\)의 입력 벡터를 \(v_w\), 출력 벡터를 \(u_w\)라고 표기하자. 그리고 확률 \(p(w\vert c)\) 을 다음과 같이 정의하자(\(\sigma\)는 시그모이드 함수).
\[p(w\vert c) := \sigma(u_w^t v_c)\]그러면 앞 절에서 보인 것처럼 \(p(w\vert c)\)는 확률 분포임을 알 수 있다. 또한 시그모이드 함수 \(\sigma\)는 \(1-\sigma(x) = \sigma(-x)\) 를 만족하므로, 위의 식 \((\star \star)\)는 다음과 같이 정리할 수 있다.
\[\text{maximize} \left(\log \sigma(u_o^t v_c) + \sum_{i=1}^{k}\log\sigma(-u_{w_i}^t v_c) \right)\]따라서 손실 함수를 다음과 같이 정의하고 그래디언트 업데이트를 수행할 수 있다.
\[J := -\log \sigma(u_o^t v_c) - \sum_{i=1}^{k}\log\sigma(-u_{w_i}^t v_c)\]네거티브 샘플링 또한 \(k\)개 정도의 계산만을 필요로 하므로 기존 소프트맥스에 비해서 계산량이 압도적으로 줄어들게 된다.
이제 문맥에 등장하지 않는 단어들을 샘플링하는 방법에 대해 논의해보자. 일반적으로 단어를 샘플링할 때는 전체 텍스트 데이터에 해당 단어가 등장하는 빈도를 이용한다. 그러나 텍스트 데이터의 경우 자주 등장하는 단어의 빈도는 그렇지 않은 단어에 비해 극도로 높은 경향이 있으므로, 네거티브 샘플 또한 특정 단어들에 치우치게 될 경향이 있다. 따라서 자주 등장하지 않는 단어가 네거티브 샘플로 선정될 확률을 높히기 위해, 네거티브 샘플은 다음 확률 분포를 이용하여 추출한다.
\[p(w) = \frac{f(w)^{3/4}}{\sum_w f(w)^{3/4}}\]여기서 \(f(w)\)는 훈련 데이터 중 단어 \(w\)의 발생 빈도이다. 또한 본 논문에서 네거티브 샘플링의 손실 함수로 주어진 다음 식은 \((\star \star)\)의 다른 표현임을 알 수 있다.
\[-\log \sigma(u_o^t v_c) - \sum_{i=1}^{k} \mathbb{E}_{w_i \sim p(w)} \left(\log\sigma(-u_{w_i}^t v_c)\right)\]여기서 \(\mathbb{E}_{w_i \sim p(w)}\) 는 단어 \(w_i\)의 샘플링 확률, 즉 기대값(Expectation)이 확률 분포가 \(p(w)\)임을 의미한다.
네거티브 샘플링에서 위의 확률 분포를 도입하는 이유를 구체적으로 예를 통해 확인해 보자. 네거티브 샘플이 is, constitution,bombastic 세 단어로 이루어져 있다고 가정하자. 다음 예는 빈도와 위 확률 사이의 관계를 나타낸다.
| 단어 | \(f(w)\) | \(p(w)\) |
|---|---|---|
| is | \(0.90\) | \(0.83\) |
| constitution | \(0.09\) | \(0.15\) |
| bombastic | \(0.01\) | \(0.03\) |
위와 같이 샘플링할 경우 빈도가 낮은 단어의 확률은 증가함을 알 수 있다. 여기서 \(3/4\)라는 값은 이론보다는 실험적으로 찾은 숫자이며, 실제로 단순 빈도나 균일 분포(모든 단어를 동일한 확률로 추출)를 사용한 경우에 비해 뛰어난 성능을 보였다고 한다.
Subsampling on Frequency
매우 큰 텍스트 데이터의 경우 in, the, a 등의 단어는 너무 자주 등장하지만 실제로는 별 의미를 담고 있지 않다. 예를 들어 France와 Paris가 같이 발생한 경우 모델의 훈련에 도움이 되지만 France와 the가 같이 발생한 경우는 큰 의미를 가지기 어렵다. 따라서 이런 단어의 발생 빈도에 따른 불균형을 해소하기 위해 서브샘플링 기법을 도입한다.
훈련 데이터로 주어진 단어 \(w\)의 발생 빈도가 \(f(w)\)인 경우, 훈련 데이터에서 해당 단어는 다음 확률로 제거하도록 한다:
\[p(w) = 1 - \sqrt{\frac{t}{f(w)}}\]여기서 \(t\)는 해당 확률을 적용하는 한계점으로, 보통 \(10^{-5}\) 정도를 사용한다. 다시 말해, 발생 빈도가 \(t\) 이하인 단어는 제거하지 않는다는 의미이다.
이런 공식을 적용하면 발생 빈도가 \(t\) 이상인 단어는 크게 제거하면서도 발생 빈도의 순서 자체는 보존하는 장점이 있다. 실제로 이렇게 서브샘플링을 적용할 경우 훈련 속도뿐 아니라 정확성까지도 크게 향상된다고 한다.
Learning Phrases
일반적으로 텍스트 데이터는 단어 단위로 토큰화하여 단어의 벡터화를 진행하게 된다. 그러나 앞서 예로 든 New York Times 등의 구절(phrase)은 New, York, Times를 각자 이해하는 경우와는 전혀 다른 의미를 가지는 고유 명사이므로 이를 묶어 하나의 토큰으로 이해할 필요가 있다. 그러나 this is 또한 연속적으로 자주 등장하는 구절이지만 이를 하나의 토큰으로 처리하기에는 적절하지 않으므로, 이 두 예제는 별도의 방법으로 처리되어야 한다.
이 논문에서는 유의미한 빈도로 연속적으로 등장하는 단어들을 하나의 토큰으로 판별하는 로직을 도입하였다. 고유명사에 포함될 수 있는 단어의 갯수는 제한이 없으므로 이론적으로는 \(n\)개의 연속된 단어의 출현 빈도를 조사하는 것이 이상적이겠으나, 현실적으로는 메모리의 제약으로 어려움이 있다. 따라서 이 논문에서는 단독으로 발생하는 빈도(unigram)와 연속으로 발생하는 빈도(bigram counting)만을 고려하여, 주어진 텍스트 데이터에서 연속한 두 단어마다 다음 점수를 계산하였다.
\[\text{score}(w_i, w_j) = \frac{f(w_i w_j) - \delta}{f(w_i) \times f(w_j)}\]여기서 \(f(w)\)는 단어 \(w\)의 빈도, \(f(w_i w_j)\)는 두 단어가 연속으로 발생하는 빈도를 의미한다.
위 식을 살펴보면, 단독으로 발생하는 빈도는 낮으나 연속으로 발생하는 빈도가 높은 단어의 점수가 높게 산출됨을 알 수 있다. 그러나 단순히 빈도가 낮은 두 단어가 우연히 연속해서 등장한 경우에도 두 단어의 점수가 높을 가능성이 있기 때문에, \(\delta\)라는 항을 도입하여 특정 빈도 이하로 연속으로 발생하는 단어는 방지하는 장치를 마련하였다. 따라서 \(\delta\) 값 이상으로 발생하는 두 단어는 고유 명사로 인정하여 하나의 토큰으로 처리한다.
또한 3개 이상의 단어로 이루어진 고유 명사 구절을 처리하기 위해, 훈련 데이터 전체에 대해 \(\delta\)를 줄여가며 2-4회 점수 산출을 반복하였다. 예를 들어 San Jose Mercury News 라는 고유명사를 생각해보자. San Jose라는 구절은 두 단어가 연속적으로 발생 확률이 높으므로 상대적으로 큰 \(\delta\) 값에서도 유의미한 구절로 판별될 가능성이 높다. 그러나 위와 같이 \(\delta\)를 줄여나가며 학습하는 경우, San Jose, Jose Mercury, Mercury News라는 두 단어로 이루어진 구절이 연속해서 등장할 확률 또한 모델이 포착하게 되므로, San Jose와 San Jose Mercury News를 다른 두 개의 고유명사로 모델이 인식할 수 있다.
위와 같은 방법을 통해 텍스트 데이터로부터 고유명사를 토큰화한 결과, 모델이 다음과 같은 고유명사 사이의 관계 또한 학습할 수 있었다고 한다.
\[\begin{array}{rcl} v_{\text{New York}} - v_{\text{New York Times}} + v_{\text{Baltimore}} &\simeq & v_{\text{Baltimore Sun}} \\ \\ v_{\text{Oakland}} - v_{\text{Golden State Warriors}} + v_{\text{Memphis}} & \simeq & v_{\text{Memphis Grizzlies}} \\ \\ v_{\text{Steve Ballmer}} - v_{\text{Microsoft}} + v_{\text{Larry Page}} & \simeq & v_{\text{Google}} \end{array}\]
Leave a comment