GloVe 모델이란?
개요
이번 글에서는 단어의 벡터화 모델 중 GloVe에 대해 이론적으로 이해해보려고 한다. GloVe 모델은 Jeffrey Pennington, Richard Socher, 그리고 Christopher D. Manning(CS224n 강의로 유명!)이 저술한 Glove: Global Vectors for Word Representation (2014) 논문에서 소개되었다. 앞으로의 내용은 이 논문을 내가 이해한 대로 풀어보려는 미약한 시도의 결과이다.
단어의 벡터 모델은 크게 SVD(singular value decomposition)를 이용한 행렬 분해 방식과 문맥에 같이 등장하는 단어들을 이용한 방법(local window method)으로 나뉜다. 전자의 대표적인 방법은 LSA(latent sementic analysis)이며, 후자로는 저번 포스트에서 소개한 Word2Vec(skip-gram) 모델 등이 있다. 그러나 두 방법은 모두 단점이 있는데, 행렬 분해 방식은 단어의 전역적 출연 빈도에 따른 통계를 활용하지만 단어간 유사성 파악에는 적합하지 않으며, skip-gram 모델은 전역적 빈도가 아닌 근방의 단어만을 이용하여 훈련된다.
저자들은 이 논문에서 단어간의 전역적 동시 등장 빈도를 토대로 훈련되는 동시에 벡터 공간의 선형성을 보존하는 모델로서 GloVe를 제안하였으며, GloVe는 단어 유사성 테스트에서 state-of-the-art 성능인 75%를 기록하였다고 한다.
단어의 유사성 테스트는 [ king : queen = man : ?? ] 라는 문제의 답을 단어에 대응되는 벡터들의 코사인 유사도를 통해 찾는 테스트이며, 자세한 내용은 이전 skip-gram 모델의 소개 포스트에 서술하였다.
GloVe 모델의 아이디어
말뭉치에서 단어의 빈도는 단어 표현의 학습에서 있어 가장 중요한 원천이라고 할 수 있다. 그러나 여전히 빈도로부터 의미가 어떻게 생성되는 지에 대해서는 여전히 많은 의문점이 남아 있다. GloVe 모델은 이런 전역적 빈도를 어떻게 활용할 지에 대한 고민에서 탄생한 모델이며, 모델의 이름부터가 Global Vectors(전역 벡터)를 줄인 것이라고 한다.
논문에서 사용되는 몇 가지 표기법을 정의하자. 본문에는 명확히 언급되어 있지 않지만, 먼저 한 단어로부터 얼마까지 떨어져있는 단어를 하나의 문맥(context)으로 인정할 것인지를 결정하는 Window size가 고정되어 있다고 하자. 이제, 단어 \(i\)의 문맥에 다른 단어 \(j\)가 등장하는 총 횟수를 \(X_{ij}\)라고 하고, 단어간 동시 발생 횟수를 나타내는 행렬 \(X\)를 다음과 같이 정의하자.
또한 \(X_i = \sum_k X_{ik}\)를 단어 \(i\)의 문맥에 등장하는 모든 단어의 총 등장 횟수라고 하자. 마지막으로, 단어 \(i\)의 문맥에 \(j\)가 등장할 확률 \(P_{ij}\)를 다음과 같이 정의하자.
\[P_{ij} := P(j\vert i) = \frac{X_{ij}}{X_i}\]GloVe 모델의 핵심 아이디어는, 두 단어 \(i\)와 \(j\)의 관계는 단순 빈도가 아니라, 또 다른 임의의 단어 \(k\)가 두 단어와 연관되어 있는 지를 분석함으로써 더욱 깊게 파악할 수 있다는 것이다. 이를 구체적인 예를 통해 이해해보자.
단어 \(i\)는 ice, \(j\)는 steam이라고 가정하자. 이 두 단어의 관계를 다양한 \(k\)에 대해 \(P_{ik}/P_{jk}\)를 계산함으로서 파악하고자 한다. 단어 \(k\)가 solid일 경우, 이 단어는 ice와는 유의미한 관계가 있으나 steam과는 그렇지 않을 것으로 예상할 수 있다. 이런 경우 \(P_{ik}/P_{jk}\)는 상대적으로 큰 값을 가질 것이다. \(k\)가 gas인 경우는 그 반대에 해당할 것이며, 단어 water와 fashion은 각각 두 단어와 모두 연관이 있거나 혹은 없는 경우에 해당한다. 실제 큰 말뭉치를 통해 계산한 각각의 확률은 다음과 같다.
| 확률 | \(k\)=solid | \(k\)=gas | \(k\)=water | \(k\)=fashion |
|---|---|---|---|---|
| \(P(k\vert \text{ice})\) | \(1.9 \times 10^{-4}\) | \(6.6\times 10^{-5}\) | \(3.0\times 10^{-3}\) | \(1.7 \times 10^{-5}\) |
| \(P(k\vert \text{steam})\) | \(2.2 \times 10^{-5}\) | \(7.8\times 10^{-4}\) | \(2.2\times 10^{-3}\) | \(1.8 \times 10^{-5}\) |
| \(P(k\vert \text{ice})/P(k\vert \text{steam})\) | \(8.9\) | \(8.5\times 10^{-2}\) | \(1.36\) | \(0.96\) |
따라서 빈도 사이의 비율을 이용하면 두 단어 중 하나와만 관련있는 단어들(solid, gas)을 두 단어 모두와 관련 있거나 없는 단어들(water, fashion)과 쉽게 분리할 수 있다. 또한 하나와만 관련 있는 단어들 또한 어떤 단어와 관련 있는지 또한 파악할 수 있다.
GloVe 모델의 구조
앞서 설명한 아이디어를 통해, 단어 표현 학습은 동시 발생 빈도 자체보다는 동시 발생 빈도 사이의 비율을 이용해야하는 것이 좋을 것이라는 기대를 가지게 되었다. 이를 구체적인 수식으로 구현해보자. 먼저 임의의 단어 \(i\)와 그 문맥에 등장하는 다른 단어 \(k\)에 대하여 \(w_i\), \(\tilde{w}_k \in \mathbb{R}^d\)를 각각 임의의 값으로 초기화된 벡터 표현이라고 가정하자(skip-gram 모델에서 \(U\), \(V\)를 임의의 값으로 초기화하는 것과 유사). 여기서 \(d\)는 벡터 공간의 차원으로, 이는 GloVe 모델의 하이퍼파라미터이다.
먼저, \(P_{ik}/P_{jk}\)라는 비율은 \(i\), \(j\), \(k\)이라는 세 단어에 의존하고 있다. 따라서 단어 모델 \(F\)의 가장 일반적인 형태는 다음과 같은 식으로 주어질 것이다.
\[F(w_i, w_j, \tilde{w}_k) = \frac{P_{ik}}{P_{jk}}\]이제 모델이 가지길 원하는 조건들을 하나씩 나열해가며 가능한 \(F\)의 형태를 좁혀 나가려고 한다. 먼저, 모델 \(F\)가 같은 벡터 공간에 존재하는 \(w_i\)와 \(w_j\) 사이의 벡터 연산을 포착할 수 있길 기대한다. 다시 말해, 모델의 값이 \(w_i\)와 \(w_j\)의 차이에만 의존하도록 만들어주기 위해 위의 수식을 다음과 같이 수정한다.
\[F(w_i-w_j, \tilde{w}_k) = \frac{P_{ik}}{P_{jk}}\]다음으로, \(F\)의 입력 변수는 벡터인 반면 결과값은 스칼라로 주어져 있다. 입력은 벡터, 결과는 스칼라인 모델은 많지만(가령 신경망), 대부분의 경우 우리가 보존하길 원하는 선형성, 즉 벡터의 연산을 보존하지 못하게 된다. 따라서 가장 간단한 형태이면서 선형성을 보존하는 벡터 내적을 다음과 같이 도입하자.
\[(\star) \quad F\left((w_i- w_j)^t \tilde{w}_k\right) = \frac{P_{ik}}{P_{jk}}\]다음으로, 단어간 동시 발생 횟수는 중심 단어와 문맥 단어의 입장이 바뀌어도 동일하므로, 행렬 \(X\)는 대칭 행렬이어야 한다(문맥은 항상 좌우를 동시에 고려한다고 가정). 따라서 모델은 \(w\)와 \(\tilde{w}\)를 서로 바꾸거나 \(X\)와 \(X^t\)를 바꾸는 경우에도 그 값이 불변이어야 한다. 그러나 현재 위에 주어진 모델은 이를 만족하지 않으므로 우리는 다음 두 추가적인 단계를 통해 대칭성을 도입하고자 한다.
먼저, \(F\)를 함수로서 이해할 때, 이 함수의 정의역은 실수 전체 집합 \(\mathbb{R}\), 공역은 음 아닌 실수 \(\mathbb{R} ^{*+} = \{ r \in \mathbb{R} \vert r> 0 \} \cup \{0\}\) 임을 알 수 있다. 또한 정의역과 공역 각각은 덧셈과 곱셈이라는 연산이 주어져 있으므로(이렇게 닫힌 연산이 주어진 집합을 군(group)이라고 함), 우리는 추가로 \(F\)가 \((\mathbb{R},+)\)에서 \((\mathbb{R}^{*+}, \times)\) 사이의 연산을 보존하길, 즉 준동형사상(homomorphism)이길 기대한다. 이를 수식으로 쓰면 다음과 같다.
\[F(a+b) = F(a) F(b) \quad \text{ for all } a, b \in \mathbb{R}\]따라서 다음 식을 얻을 수 있고
\[(\star\star)\quad F\left((w_i- w_j)^t \tilde{w}_k\right) = \frac{F(w_i^t \tilde{w}_k)}{F(w_j^t \tilde{w}_k)},\]위에서 정의한 \((\star)\)와 위 식을 비교하면 \(F\)가 다음을 만족하는 것이 자연스럽다.
\[F(w_i^t \tilde{w}_k) = P_{ik} = \frac{X_{ik}}{X_i}\]위 \((\star\star)\)를 만족하는 \(F\)는 여러가지가 있지만, 가장 간단한 지수 함수를 사용하기로 한다. 다시 말해,
\[w_i^t \tilde{w}_k = \log(P_{ik}) = \log(X_{ik}) - \log(X_i)\]가 성립한다.
그러나 위 식 또한 \(\log(X_i)\)의 존재로 인하여 \(w_i\)와 \(\tilde{w}_k\) 사이의 대칭성을 보존하지 않는다. 그러나 \(\log(X_i)\) 자체는 \(k\)에 의존하지 않으므로 이를 \(i\)에만 의존하는 편향(bias) \(b_i\)라 가정할 수 있다. 여기에 추가로 \(\tilde{w}_k\)에 의존하는 편향 \(\tilde{b}_k\)를 더하면 위 식은 다음과 같이 정리할 수 있다.
\[w_i^t \tilde{w}_k + b_i + \tilde{b}_k = \log(X_{ik})\]결국, GloVe 모델의 목표는 모든 단어 \(i\)와 \(k\)에 대해 위 식을 최대한 만족하는 단어의 벡터 표현 \(w\), \(\tilde{w}\) (와 편향 \(b, \tilde{b}\))을 찾는 것이다.
GloVe 모델의 학습 방법
앞서 설명한 GloVe 모델의 구조로부터, 결국 우리는 다음을 최소화하는 방향으로 모델을 훈련시켜야 한다는 것을 알 수 있다(\(V\)는 말뭉치에 등장하는 단어의 총 갯수).
\[\sum_{i,j}^V \left(w_i^t \tilde{w}_j + b_i + \tilde{b}_j - \log(X_{ij}) \right)^2\]그러나 여기엔 큰 문제가 있는데, 바로 로그 함수는 입력값이 \(0\)으로 가까워지면 발산한다는 점이다. 실제 \(X_{ik}\)는 많은 \(i, k\)에 대해 \(0\)이므로, 이를 해결하기 위하여 새로운 함수 \(f\)를 도입하여 다음 식을 GloVe 모델의 손실 함수로 정의하고자 한다.
\[J := \sum_{i,j}^V f(X_{ij})\left(w_i^t \tilde{w}_j + b_i + \tilde{b}_j - \log X_{ij} \right)^2\]앞서 말한 로그의 발산 문제를 해결하기 위해, 또한 모델의 합리성을 증가시키기 위해 \(f\)는 다음 성질들을 만족해야 한다.
-
- \(f(0) = 0\)
- \(f\)는 로그 함수가 \(0\) 근처에서 발산하는 속도보다 빠르게 \(0\)으로 수렴해야 한다.
-
- \(f(x)\)는 증가 함수
- 빈도가 증가할 수록 모델에 끼치는 영향력이 증가해야 한다.
-
- \(f(x)\)는 상한을 가져야 함
- 자주 등장하는 단어가 너무 큰 영향력을 가져서는 안된다.
GloVe 모델의 경우 위 성질을 만족하는 함수 \(f\)를 다음과 같이 정의하였다.
\[f(x) = \left\{ \begin{array}{cl} (x/x_{\text{max}})^\alpha & \text{if } x< x_{\text{max}} \\ 1 & \text{otherwise.} \end{array} \right.\]그리고 하이퍼파라미터 \(x_{\text{max}}=100\), \(\alpha=3/4\)를 사용했다고 하며, 이 경우 \(f(x)\)의 그래프는 다음과 같다.
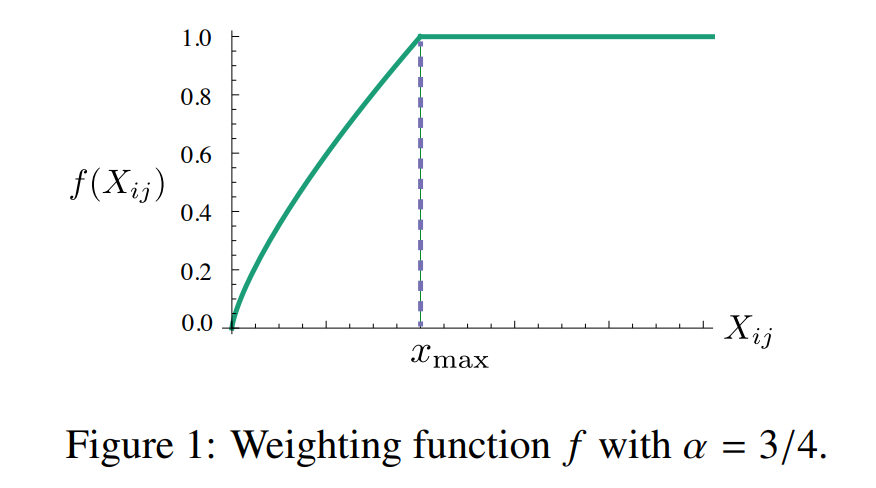
[source : https://lovit.github.io/assets/figures/glove-weighting-function.png]
정리하면 GloVe 모델은 말뭉치에 등장하는 단어에 대한 두 벡터 표현 \(w, \tilde{w} \in \mathbb{R}^d\)(과 편향 \(b, \tilde{b} \in \mathbb{R})\)를 임의의 값으로 초기화 한 후, 위의 손실 함수 \(J\)를 최소화하는 방향으로 훈련해나가는 모델이다.
GloVe 모델의 복잡도
GloVe 모델의 복잡도는 동시 발생 행렬 \(X\)에서 \(0\)이 아닌 원소의 갯수에 의존한다. 이런 원소의 수는 전체 원소의 수인 \(\vert V \vert^2\) 보다 작으므로, GloVe 모델의 복잡도는 최대 \(O(\vert V \vert^2)\) 이다. Skip-gram 같은 모델의 복잡도는 전체 말뭉치의 크기인 \(\vert C \vert\) 에 비례하므로 얼핏 보기엔 GloVe 모델의 복잡도가 더 나은 것으로 보이기 쉬우나, 실제 사용되는 단어의 크기 \(\vert V \vert\) 가 보통 \(10^6\) 이상이므로, 이런 경우 \(\vert V \vert^2\) 는 약 \(10^{12} = 1\)조(!)에 해당하는 어마어마한 수치가 되어버린다. 따라서 GloVe 모델의 실제 복잡도를 계산하기 위해서는 \(X\)의 \(0\) 아닌 원소의 갯수(=\(\vert X \vert\))에 대한 좀 더 정밀한 상한을 구할 필요가 있다.
이를 수행하기 위해 우리는 단어의 동시 발생 분포에 대해 다음을 가정하고자 한다.
임의의 단어 \(i\), \(j\)에 대하여, (\(i\),\(j\))라는 단어쌍의 빈도가 전체 단어쌍 중 \(r_{ij}\) 번째로 많이 등장한다고 가정할 때, 어떤 상수 \(k\)와 양수 \(\alpha\)가 존재하여 다음이 성립한다.
\[X_{ij} ~\sim~ \frac{k}{(r_{ij})^\alpha}\]여기서 \(a \sim b\) 는 어떤 상수 \(t\)가 존재하여 \(\vert a \vert \le t \vert b\vert\) 임을 의미한다.
말뭉치에 등장하는 전체 단어의 수 \(\vert C \vert\)는 동시 등장 행렬 \(X\)의 모든 원소의 합에 비례하므로 다음이 성립한다.
\[\vert C \vert~ \sim~ \sum_{i,j}X_{ij} ~\sim~ \sum_{r=1}^{\vert X \vert } \frac{k}{r^\alpha}~ = ~k H_{\vert X \vert, \alpha}\]여기서 \(H_{n,m} = \sum_{r=1}^n \frac{1}{r^m}\) 로 정의되는 조화수(harmonic number)이다. 또한 \(\vert X \vert\)에 대해 다음과 같이 표현할 수 있다.
\[\vert X \vert = \max_{i,j} \{ r_{ij} \vert X_{ij} > 0 \} = \max_{i,j} \{ r_{ij} \vert X_{ij} = 1 \} \sim k^{1/\alpha}\]따라서 위 두 식을 결합하면 다음 식을 얻을 수 있다.
\[\vert C \vert ~ \sim ~ \vert X \vert ^\alpha H_{\vert X \vert, \alpha}\]이 식을 추가로 전개하기 위하여 조화수에 대한 다음 근사식을 사용하자(Apostol, 1976).
\(\zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^s}\) 를 리만 제타 함수라고 하자. 그러면 조화수 \(H_{x,s}\)는 다음과 같이 근사할 수 있다.
\[H_{x,s} = \frac{x^{1-s}}{1-s} + \zeta(s) + \mathcal{O}(x^{-s})\quad \text{ if } s>0 , s\ne 1\]
위 식을 \(\vert C \vert\)의 근사식에 대입하면 다음이 된다.
\[\vert C \vert \sim \frac{\vert X \vert}{1-\alpha} + \zeta(\alpha) \vert X \vert ^\alpha + \mathcal{O}(1)\]우리는 \(\vert X \vert\)가 큰 수일 경우에 대해 관심 있으므로 \(\vert X \vert >1\) 라고 가정할 수 있고, 따라서 우리는 \(\vert X \vert\)의 계산 복잡도를 다음과 같이 얻을 수 있다.
\[\vert X \vert \left\{ \begin{array}{cl}\mathcal{O}(\vert C \vert) & \text{ if } \alpha < 1 \\ \mathcal{O}(\vert C \vert^{1/\alpha}) & \text{ if } \alpha >1 \end{array}\right.\]GloVe 모델의 경우 \(\alpha = 1.25\) 를 사용하면 \(X_{ij} \sim \frac{k}{r_{ij}^\alpha}\) 로 모델링이 잘 이루어졌다고 한다. 따라서 이 경우 모델의 계산 복잡도는 \(\vert X \vert = \mathcal{O}(\vert C \vert ^{0.8})\) 을 얻을 수 있으며, 따라서 skip-gram 모델의 복잡도 \(\mathcal{O}(\vert C \vert)\)에 비해 개선된 결과임을 알 수 있다.

Leave a comment