AFM (Attentional Factorization Machines)

• 논문 제목 : Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks, Xiao et al. (2017)
• 구현 코드

FM(Factorization Machines)은 행렬분해를 일반화한 모델로서, 각 feature들의 value를 모두 one-hot-encoding으로 변환하여 얻은 입력 벡터 \(\mathbf{x} \in \mathbb{R}^n\) 으로 부터 output \(\hat{y}\) 을 다음 식을 통해 얻는다.

\[\hat{y}(\mathbf{x}) = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n\sum_{j=i+1}^n \hat{w}_{ij}x_i x_j.\]

여기서 \(\hat{w}_{ij}\)는 feature \(i\)에 대응되는 벡터 \(\mathbf{v}_i \in \mathbb{R}^k\)와 \(\mathbf{v}_j\)의 dot-product이다.

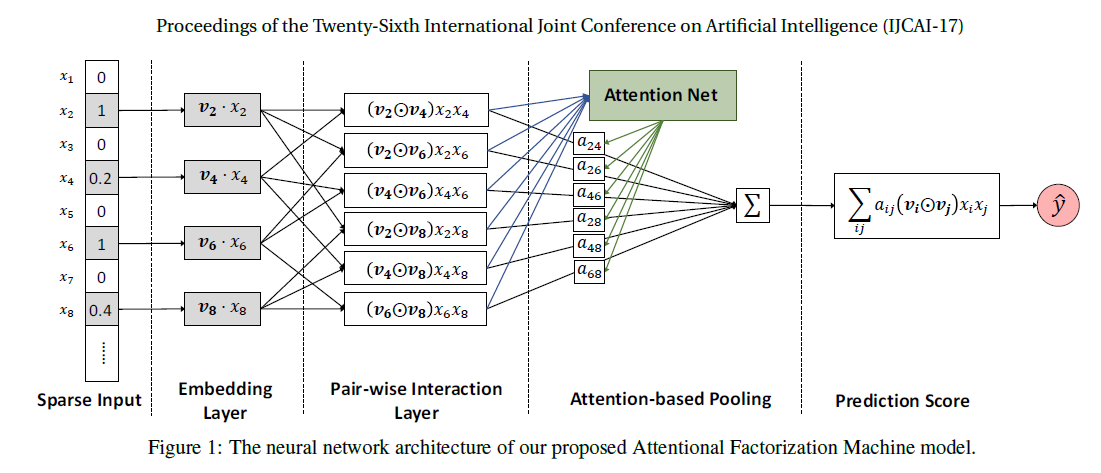
AFM(Attentional Factorization Machines)은 FM에 Attention을 추가로 적용하여 일반화한 모델이며, 이를 통해 각 feature별로 출력에 끼치는 영향력을 다르게 반영할 수 있다. 입력 \(\mathbf{x}\)에 대응하는 출력 \(\hat{y}_{\text{AFM}}(\mathbf{x})\)는 다음과 같이 정의된다.

\[\hat{y}_{\text{AFM}}(\mathbf{x}) = w_0 + \sum_{i=1}^n w_i x_i + \mathbf{p}^T\sum_{i=1}^n\sum_{j=i+1}^n a_{ij}(\mathbf{v}_i \odot \mathbf{v}_j ) x_i x_j, \\ a_{ij} = \frac{\exp(a_{ij}^\prime)}{\sum_{(i,j)\in\mathfrak{R}_\mathbf{x}} \exp(a_{ij}^\prime)}, ~ a_{ij}^\prime = \mathbf{h}^T \text{ReLU}(\mathbf{W}(\mathbf{v}_i\odot \mathbf{v}_j)x_i x_j + \mathbf{b}).\]

여기서,

\[\mathfrak{R}_\mathbf{x} = \{(i,j)~\vert~ x_ix_j >0 \text{ and } j>=i+1 \},\\ \mathbf{p} \in \mathbb{R}^k, \mathbf{W} \in \mathbb{R}^{t \times k}, \mathbf{b, h}\in \mathbb{R}^t\]

이다. 그리고 Loss function은 다음과 같이 정의된다.

\[L = \sum_\mathbf{x} (\hat{y}_{\text{AFM}}(\mathbf{x}) - y(\mathbf{x}))^2 + \lambda \|\mathbf{W}\|^2.\]